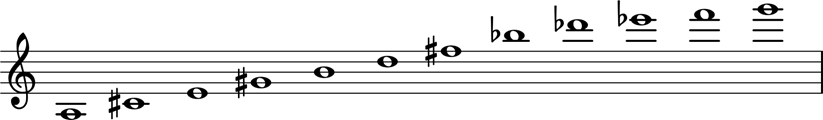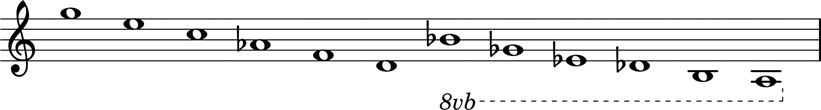Primera mitad del Siglo XX. El neoclasicismo, el atonalismo y la 2ª Escuela de Viena
2. Ruptura con la tonalidad
2.3. La Segunda Escuela de Viena
2.3.1. El dodecafonismo
El dodecafonismo, o serialismo, es una técnica de composición que surgió en la primera mitad del siglo XX. Fue desarrollado principalmente por el compositor austríaco Arnold Schoenberg. La idea principal detrás de esta técnica es la organización de las doce notas de la escala cromática en una serie o serie dodecafónica, que luego se utiliza como base para la composición. Esta técnica rompe con la tradición tonal que había dominado la música occidental desde el siglo XVII.
La idea era que la música tonal diera el máximo protagonismo a un sonido: la tónica. Pero estos nuevos compositores buscaron “una democracia de sonidos” en la que todos los sonidos fueran iguales, sin que ninguno fuera jerárquicamente más importante que los demás.
Para construir una serie de doce sonidos, se elabora una lista de los doce sonidos, usando cada uno exactamente una vez y nunca repitiendo ninguno. A continuación podemos ver la serie original del Concierto para violín de Berg.

|
Serie original |
Esta serie es solo una lista de alturas; pudiendo aparecer en cualquier registro, de manera melódica y/o armónica o dividida en distintos instrumentos de un ensemble.

El ejemplo anterior muestra el concepto de equivalencia de octavas. La equivalencia de octava establece que no es necesario tocar una nota en una octava determinada.
2.3.2. Variaciones de una serie dodecafónica
A partir de esa forma original de la serie, hay cuatro transformaciones cardinales que se usan para cambiar la serie original en otra cosa.
Transposición: En primer lugar, podemos transponerlo para comenzar en cualquier otra altura.
|
Serie transportada una 2ª M ascendente |
Retrogradación: También podemos retrogradarlo, lo que significa que lo escribimos al revés.
|
Serie retrogradada |
Inversión: Podemos invertirlo, lo que significa que usamos los intervalos de la forma original de la serie, pero vamos en la dirección opuesta:
|
Serie invertida |
Inversión retrogradada: También podemos invertirlos y retrogradarlos, que es una combinación de las dos transformaciones anteriores. La siguiente serie es simplemente la forma de la serie invertida retrógrada.
|
Serie invertida retrogradada |
Por último, podemos combinar cualquiera de estas transformaciones, dando lugar a 48 posibles series.
2.3.3. Matriz de doce tonos
Los compositores y teóricos a menudo usan una herramienta llamada matriz de doce tonos para determinar todas las posibles variaciones de una serie. Esto forma una matriz de 48 posibles variaciones de en una cuadrícula de 12 por 12.
|
|
I0↓ |
I1↓ |
I6↓ |
I7↓ |
I5↓ |
I2↓ |
I4↓ |
I3↓ |
I10↓ |
I9↓ |
I11↓ |
I8↓ |
|
|
P0→ |
Do |
Re♭ |
Sol♭ |
Sol |
Fa |
Re |
Mi |
Mi♭ |
Si♭ |
La |
Si |
Sol♯ |
←R0 |
|
P11→ |
Si |
Do |
Fa |
Sol♭ |
Mi |
Re♭ |
Mi♭ |
Re |
La |
La♭ |
Si♭ |
Sol |
←R11 |
|
P6→ |
Sol♭ |
Sol |
Do |
Re♭ |
Si |
La♭ |
Si♭ |
La |
Mi |
Mi♭ |
Fa |
Re |
←R6 |
|
P5→ |
Fa |
Sol♭ |
Si |
Do |
Si♭ |
Sol |
La |
La♭ |
Mi♭ |
Re |
Mi |
Do♯ |
←R5 |
|
P7→ |
Sol |
La♭ |
Re♭ |
Re |
Do |
La |
Si |
Si♭ |
Fa |
Mi |
Sol♭ |
Mi♭ |
←R7 |
|
P10→ |
Si♭ |
Si |
Mi |
Fa |
Mi♭ |
Do |
Re |
Re♭ |
La♭ |
Sol |
La |
Fa♯ |
←R10 |
|
P8→ |
La♭ |
La |
Re |
Mi♭ |
Re♭ |
Si♭ |
Do |
Si |
Fa♯ |
Fa |
Sol |
Mi |
←R8 |
|
P9→ |
La |
Si♭ |
Mi♭ |
Mi |
Re |
Si |
Do♯ |
Do |
Sol |
Sol♭ |
La♭ |
Fa |
←R9 |
|
P2→ |
Re |
Mi♭ |
La♭ |
La |
Sol |
Mi |
Fa♯ |
Fa |
Do |
Si |
Re♭ |
Si♭ |
←R2 |
|
P3→ |
Mi♭ |
Mi |
La |
Si♭ |
La♭ |
Fa |
Sol |
Sol♭ |
Re♭ |
Do |
Re |
Si |
←R3 |
|
P1→ |
Re♭ |
Re |
Sol |
La♭ |
Sol♭ |
Mi♭ |
Fa |
Mi |
Si |
Si♭ |
Do |
La |
←R1 |
|
P4→ |
Mi |
Fa |
Si♭ |
Si |
La |
Sol♭ |
La♭ |
Sol |
Re |
Re♭ |
Mi♭ |
Do |
←R4 |
|
|
↑Ri0 |
↑Ri1 |
↑Ri6 |
↑Ri7 |
↑Ri5 |
↑Ri2 |
↑Ri4 |
↑Ri3 |
↑Ri10 |
↑Ri9 |
↑Ri11 |
↑Ri8 |
|
Para construir una matriz, escribe la serie original (P) de izquierda a derecha en la fila superior, luego escribe la forma invertida (I) de arriba a abajo en la columna de la izquierda. A partir de ahí, puedes escribir las transposiciones de la forma original, dadas las notas iniciales en la columna de la izquierda. Uno continuaría con cada transposición de la forma original hasta que la matriz esté completa.
|
|
I0↓ |
I1↓ |
I6↓ |
I7↓ |
I5↓ |
I2↓ |
I4↓ |
I3↓ |
I10↓ |
I9↓ |
I11↓ |
I8↓ |
|
|
P0→ |
Do |
Re♭ |
Sol♭ |
Sol |
Fa |
Re |
Mi |
Mi♭ |
Si♭ |
La |
Si |
Sol♯ |
←R0 |
|
P11→ |
Si |
|
|
|
|
|
|
|
|
|
|
|
←R11 |
|
P6→ |
Sol♭ |
|
|
|
|
|
|
|
|
|
|
|
←R6 |
|
P5→ |
Fa |
|
|
|
|
|
|
|
|
|
|
|
←R5 |
|
P7→ |
Sol |
|
|
|
|
|
|
|
|
|
|
|
←R7 |
|
P10→ |
Si♭ |
|
|
|
|
|
|
|
|
|
|
|
←R10 |
|
P8→ |
La♭ |
|
|
|
|
|
|
|
|
|
|
|
←R8 |
|
P9→ |
La |
|
|
|
|
|
|
|
|
|
|
|
←R9 |
|
P2→ |
Re |
|
|
|
|
|
|
|
|
|
|
|
←R2 |
|
P3→ |
Mi♭ |
|
|
|
|
|
|
|
|
|
|
|
←R3 |
|
P1→ |
Re♭ |
|
|
|
|
|
|
|
|
|
|
|
←R1 |
|
P4→ |
Mi |
|
|
|
|
|
|
|
|
|
|
|
←R4 |
|
|
↑Ri0 |
↑Ri1 |
↑Ri6 |
↑Ri7 |
↑Ri5 |
↑Ri2 |
↑Ri4 |
↑Ri3 |
↑Ri10 |
↑Ri9 |
↑Ri11 |
↑Ri8 |
|